二叉搜索树(Binary Search Tree)简称 BST,是二叉树的一种特殊形式。它有很多别名,比如排序二叉树、二叉查找树等等。
虽然二叉搜索树多年来一直作为算法面试的“必要考点”存在,但在实际面试中,它的考察频率并不能和常规二叉树相提并论,算不上“大热”的考点,同时考察内容也是相对比较稳定的。对于二叉搜索树,我们只要能够把握好它的限制条件和特性,就足以应对大部分的考题。
# 什么是二叉搜索树
树的定义总是以递归的形式出现,二叉搜索树也不例外,它的递归定义如下:
- 是一棵空树
- 是一棵由根结点、左子树、右子树组成的树,同时左子树和右子树都是二叉搜索树,且左子树上所有结点的数据域都小于等于根结点的数据域,右子树上所有结点的数据域都大于等于根结点的数据域
满足以上两个条件之一的二叉树,就是二叉搜索树。
从这个定义我们可以看出,二叉搜索树强调的是数据域的有序性。也就是说,二叉搜索树上的每一棵子树,都应该满足
左孩子 <= 根结点 <= 右孩子这样的大小关系。下图我给出了几个二叉搜索树的示例
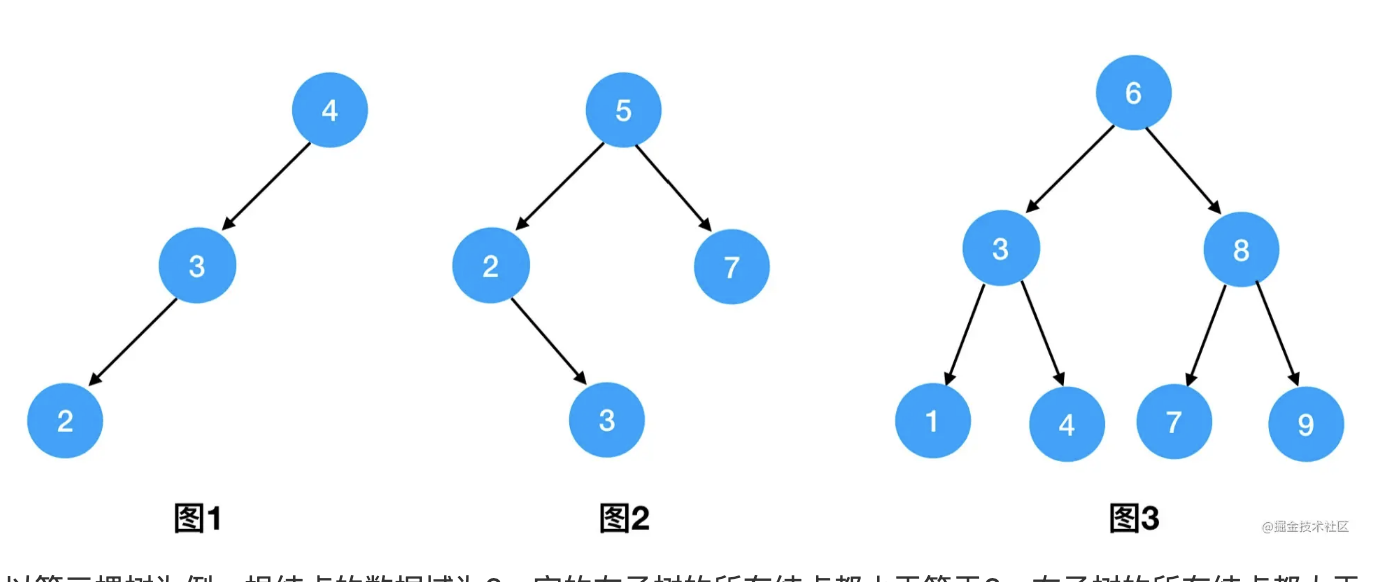
以第三棵树为例,根结点的数据域为6,它的左子树的所有结点都小于等于6、右子树的所有结点都大于等于6。同时在任意子树的内部,也满足这个条件——比如左子树中,根结点值为3,根结点对应左子树的所有结点都小于等于3、右子树的所有结点都大于等于3。
# 二叉搜索树:编码基本功
关于二叉搜索树,大家需要掌握以下高频操作:
- 查找数据域为某一特定值的结点
- 插入新结点
- 删除指定结点
# 查找数据域为某一特定值的结点
假设这个目标结点的数据域值为 n,我们借助二叉搜索树数据域的有序性,可以有以下查找思路:
- 递归遍历二叉树,若当前遍历到的结点为空,就意味着没找到目标结点,直接返回。
- 若当前遍历到的结点对应的数据域值刚好等于n,则查找成功,返回。
- 若当前遍历到的结点对应的数据域值大于目标值n,则应该在左子树里进一步查找,设置下一步的遍历范围为 root.left 后,继续递归。
- 若当前遍历到的结点对应的数据域值小于目标值n,则应该在右子树里进一步查找,设置下一步的遍历范围为 root.right 后,继续递归。
编码实现
function search(root, n) {
// 若 root 为空,查找失败,直接返回
if(!root) {
return
}
// 找到目标结点,输出结点对象
if(root.val === n) {
console.log('目标结点是:', root)
} else if(root.val > n) {
// 当前结点数据域大于n,向左查找
search(root.left, n)
} else {
// 当前结点数据域小于n,向右查找
search(root.right, n)
}
}
# 插入新结点
插入结点的思路其实和寻找结点非常相似。大家反思一下,在上面寻找结点的时候,为什么我们会在判定当前结点为空时,就认为查找失败了呢? 这是因为,二叉搜索树的查找路线是一个非常明确的路径:我们会根据当前结点值的大小,决定路线应该是向左走还是向右走。如果最后走到了一个空结点处,这就意味着我们没有办法再往深处去搜索了,也就没有了找到目标结点的可能性。
换一个角度想想,如果这个空结点所在的位置恰好有一个值为 n 的结点,是不是就可以查找成功了?那么如果我把 n 值塞到这个空结点所在的位置,是不是刚好符合二叉搜索树的排序规则?
实不相瞒,二叉搜索树插入结点的过程,和搜索某个结点的过程几乎是一样的:从根结点开始,把我们希望插入的数据值和每一个结点作比较。若大于当前结点,则向右子树探索;若小于当前结点,则向左子树探索。最后找到的那个空位,就是它合理的栖身之所。
编码实现
function insertIntoBST(root, n) {
// 若 root 为空,说明当前是一个可以插入的空位
if(!root) {
// 用一个值为n的结点占据这个空位
root = new TreeNode(n)
return root
}
if(root.val > n) {
// 当前结点数据域大于n,向左查找
root.left = insertIntoBST(root.left, n)
} else {
// 当前结点数据域小于n,向右查找
root.right = insertIntoBST(root.right, n)
}
// 返回插入后二叉搜索树的根结点
return root
}
# 删除指定结点
想要删除某个结点,首先要找到这个结点。在定位结点后,我们需要考虑以下情况:
- 结点不存在,定位到了空结点。直接返回即可。
- 需要删除的目标结点没有左孩子也没有右孩子——它是一个叶子结点,删掉它不会对其它结点造成任何影响,直接删除即可。
- 需要删除的目标结点存在左子树,那么就去左子树里寻找小于目标结点值的最大结点,用这个结点覆盖掉目标结点
- 需要删除的目标结点存在右子树,那么就去右子树里寻找大于目标结点值的最小结点,用这个结点覆盖掉目标结点
- 需要删除的目标结点既有左子树、又有右子树,这时就有两种做法了:要么取左子树中值最大的结点,要么取右子树中取值最小的结点。两个结点中任取一个覆盖掉目标结点,都可以维持二叉搜索树的数据有序性
编码实现
function deleteNode(root, n) {
// 如果没找到目标结点,则直接返回
if(!root) {
return root
}
// 定位到目标结点,开始分情况处理删除动作
if(root.val === n) {
// 若是叶子结点,则不需要想太多,直接删除
if(!root.left && !root.right) {
root = null
} else if(root.left) {
// 寻找左子树里值最大的结点
const maxLeft = findMax(root.left)
// 用这个 maxLeft 覆盖掉需要删除的当前结点
root.val = maxLeft.val
// 覆盖动作会消耗掉原有的 maxLeft 结点
root.left = deleteNode(root.left, maxLeft.val)
} else {
// 寻找右子树里值最小的结点
const minRight = findMin(root.right)
// 用这个 minRight 覆盖掉需要删除的当前结点
root.val = minRight.val
// 覆盖动作会消耗掉原有的 minRight 结点
root.right = deleteNode(root.right, minRight.val)
}
} else if(root.val > n) {
// 若当前结点的值比 n 大,则在左子树中继续寻找目标结点
root.left = deleteNode(root.left, n)
} else {
// 若当前结点的值比 n 小,则在右子树中继续寻找目标结点
root.right = deleteNode(root.right, n)
}
return root
}
// 寻找左子树最大值
function findMax(root) {
while(root.right) {
root = root.right
}
return root
}
// 寻找右子树的最小值
function findMin(root) {
while(root.left) {
root = root.left
}
return root
}
# 编码复盘
上面这段代码展示了二叉搜索树删除的基本思路:在这个思路的基础上,大家可以做很多个性化的修改。
举个例子,细心的同学会发现,如果目标结点既有左子树又有右子树,那么在上面这段逻辑里,会优先去找它左子树里的最大值,而不会去 care 右子树的最小值这个选项。
这样做,得到的结果从正确性上来说是没问题的,但是却不太美观:每次都删除一侧子树的结点,会导致二叉树的左右子树高度不平衡。
如果题目中要求我们顾及二叉树的平衡度,那么我们就可以在删除的过程中记录子树的高度,每次选择高度较高的子树作为查找目标,用这个子树里的结点去覆盖需要删除的目标结点。
# 二叉搜索树的特性
关于二叉搜索树的特性,有且仅有一条是需要大家背诵默写的:
二叉搜索树的中序遍历序列是有序的!
OK,基本功就修炼到这里,下面大家一起来开开心心地碾碎真题吧!
# 真题实战环节
开篇我们说过,我们只要能够把握好二叉搜索树的限制条件(即定义)和特性,就足以应对大部分的考题。下面我们就来看看定义和特性的考察是如何在真题中体现的:
# 对定义的考察:二叉搜索树的验证
题目描述:给定一个二叉树,判断其是否是一个有效的二叉搜索树。
- 假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
示例 2:
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4
思路分析
对于这道题,我们需要好好咀嚼一下二叉搜索树的定义:
- 它可以是一棵空树
- 它可以是一棵由根结点、左子树、右子树组成的树,同时左子树和右子树都是二叉搜索树,且左子树上所有结点的数据域都小于等于根结点的数据域,右子树上所有结点的数据域都大于等于根结点的数据域
只有符合以上两种情况之一的二叉树,可以称之为二叉搜索树。
空树的判定比较简单,关键在于非空树的判定:需要递归地对非空树中的左右子树进行遍历,检验每棵子树中是否都满足 左 < 根 < 右 这样的关系(注意题中声明了不需要考虑相等情况)。
基于这样的思路,我们可以编码如下:
编码实现
/**
* @param {TreeNode} root
* @return {boolean}
*/
const isValidBST = function(root) {
// 定义递归函数
function dfs(root, minValue, maxValue) {
// 若是空树,则合法
if(!root) {
return true
}
// 若右孩子不大于根结点值,或者左孩子不小于根结点值,则不合法
if(root.val <= minValue || root.val >= maxValue) return false
// 左右子树必须都符合二叉搜索树的数据域大小关系
return dfs(root.left, minValue,root.val) && dfs(root.right, root.val, maxValue)
}
// 初始化最小值和最大值为极小或极大
return dfs(root, -Infinity, Infinity)
};
编码复盘
这个题的编码实现比较有意思,对 minValue 和 maxValue 的处理值得我们反刍一下:
递归过程中,起到决定性作用的是这两个判定条件:
- 左孩子的值是否小于根结点值
- 右孩子的值是否大于根结点值
在递归式中,如果单独维护一段逻辑,用于判定当前是左孩子还是右孩子,进而决定是进行大于判定还是小于判定,也是没问题的。但是在上面的编码中我们采取了一种更简洁的手法,通过设置 minValue 和 maxValue 为极小和极大值,来确保 root.val <= minValue || root.val >= maxValue 这两个条件中有一个是一定为 false 的。
比如当前我需要检查的是root 的左孩子,那么就会进入 dfs(root.left, minValue,root.val) 这段逻辑。这个dfs调用将最大值更新为了root根结点的值,将当前root结点更新为了左孩子结点,同时保持最小值为 -Infinity 不变。进入 dfs逻辑后,root.val <= minValue || root.val >= maxValue 中的 root.val <= minValue 一定为 false ,起决定性作用的条件实际是 root.val >= maxValue(这里这个 maxValue 正是根结点的数据域值)。若root.val >= maxValue返回 true,就意味着左孩子的值大于等于(也就是不小于)根结点的数据域值,这显然是不合法的。此时整个或语句都会返回true,递归式返回false,二叉搜索树进而会被判定为不合法。
# 对特性的考察:将排序数组转化为二叉搜索树
题目描述:将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
- 给定有序数组: [-10,-3,0,5,9],
- 一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0
/ \
-3 9
/ /
-10 5
思路分析
这道题出现在这个位置真是太棒了(陶醉脸),它不仅是一道典型的二叉搜索树应用题,还涉及到了平衡二叉树的基本知识,对下一个专题的学习起到了很好的铺垫作用。
做这个题,大家可以先观察一下它的输入和输出,你会发现它们之间有着很微妙的关系。先看输入:
[-10,-3,0,5,9]
再看输出:
0
/ \
-3 9
/ /
-10 5
- 这个二叉树从形状上来看,像不像是把数组从 0 这个中间位置给“提起来”了?
- 别笑,我们接下来要做的事情,还真就是要想办法把这个数组给“提”成二叉树。
在想办法之前,我们先来反思一下为什么可以通过“提起来”来实现数组到目标二叉树的转换,这里面蕴含了两个依据:
- 二叉搜索树的特性:题目中指明了目标树是一棵二叉搜索树,二叉搜索树的中序遍历序列是有序的,题中所给的数组也是有序的,因此我们可以认为题目中给出的数组就是目标二叉树的中序遍历序列。中序遍历序列的顺序规则是 左 -> 根 -> 右,因此数组中间位置的元素一定对应着目标二叉树的根结点。以根结点为抓手,把这个数组“拎”起来,得到的二叉树一定是符合二叉搜索树的排序规则的。
- 平衡二叉树的特性:虽然咱们还没有讲啥是平衡二叉树,但是题目中已经妥妥地给出了一个平衡二叉树的定义:
一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
要做到这一点,只需要把“提起来”这个动作贯彻到底就行了:当我们以有序数组的中间元素为根结点,“提”出一个二叉树时,有两种可能的情况:
数组中元素为奇数个,此时以数组的中间元素为界,两侧元素个数相同:
[-10,-3,0,5,9]
如果我们以中间元素为根结点,把数组“提”成二叉树,那么根结点左右两侧的元素个数是一样的,所以站在根结点来看,左右子树的高度差为0:
0
/ \
-3 9
/ /
-10 5
数组中元素为偶数个,此时无论是选择中间靠左的元素为界、还是选择中间靠右的元素为界,两侧元素个数差值的绝对值都是1:
[-10,-3,0,5]
在这个例子里,若以 -3 为根结点,那么左右子树的高度差的绝对值就是1:
-3
/ \
-10 0
\
5
以 0 为根结点亦然。
通过对以上情况进行探讨,我们发现“以中间元素为根结点,将数组提成树”这种操作,可以保证根结点左右两侧的子树高度绝对值不大于1。要想保证每一棵子树都满足这个条件,我们只需要对有序数组的每一个对半分出来的子序列都递归地执行这个操作即可
编码实现
/**
* @param {number[]} nums
* @return {TreeNode}
*/
const sortedArrayToBST = function(nums) {
// 处理边界条件
if(!nums.length) {
return null
}
// root 结点是递归“提”起数组的结果
const root = buildBST(0, nums.length-1)
// 定义二叉树构建函数,入参是子序列的索引范围
function buildBST(low, high) {
// 当 low > high 时,意味着当前范围的数字已经被递归处理完全了
if(low > high) {
return null
}
// 二分一下,取出当前子序列的中间元素
const mid = Math.floor(low + (high - low)/2)
// 将中间元素的值作为当前子树的根结点值
const cur = new TreeNode(nums[mid])
// 递归构建左子树,范围二分为[low,mid)
cur.left = buildBST(low,mid-1)
// 递归构建左子树,范围二分为为(mid,high]
cur.right = buildBST(mid+1, high)
// 返回当前结点
return cur
}
// 返回根结点
return root
};