# 二叉树概述
# 二叉树概述
二叉树是非常基础并且是一种非常重要的数据结构, 正和它的名字一样, 二叉树的每个节点最多有两个子树.
我们可以先来看下面的这颗二叉树, 为了方便,我这里将left用L表示, right用R表示:
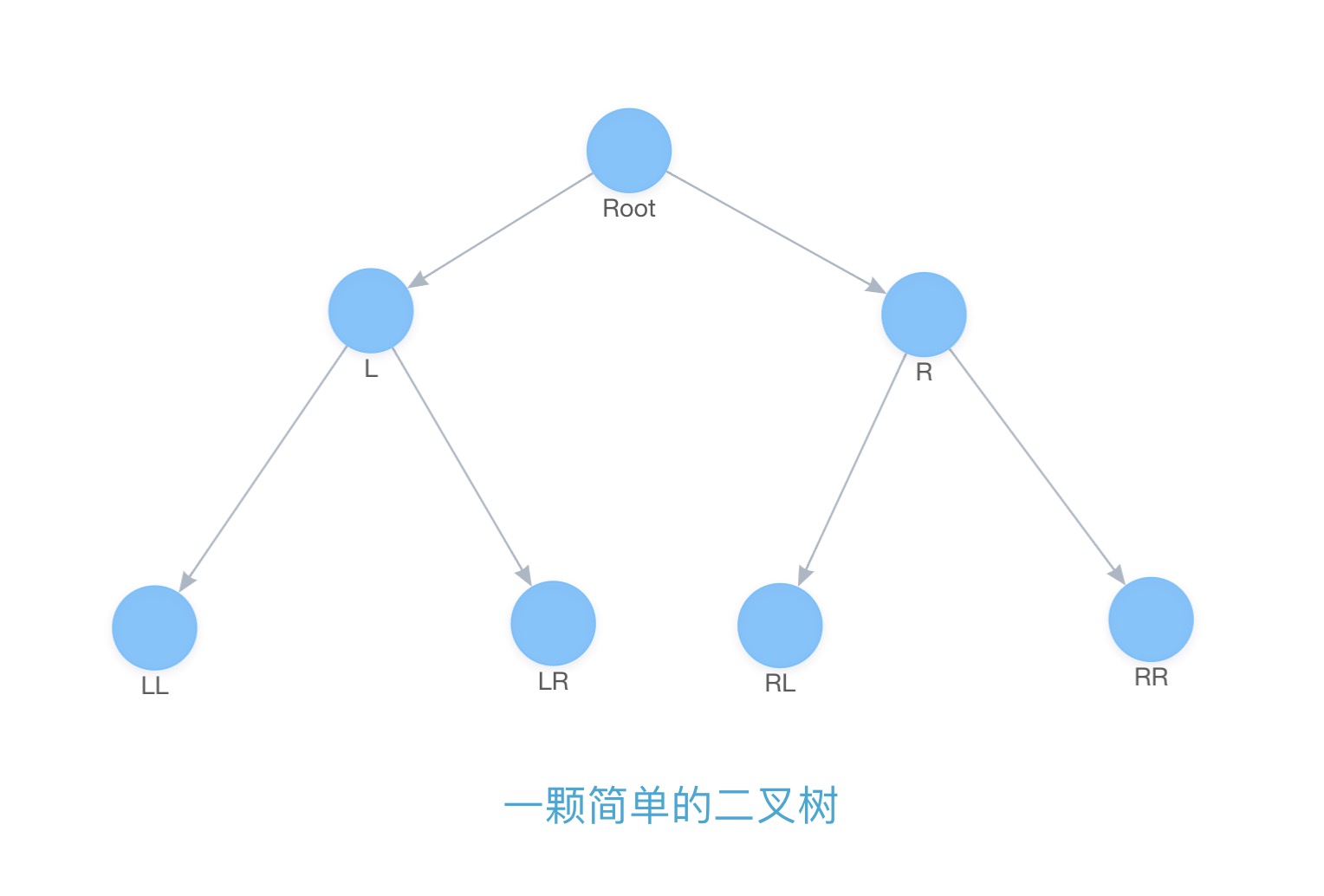
# 二叉树与JS
上面的二叉树可以用我们JavaScript的对象来进行表示, 相信大家很容易就能看懂:
var tree = {
value: "Root",
left: {
value: 'L',
left: {
value: 'LL'
},
right: {
value: 'LR'
}
},
right: {
value: 'R',
left: {
value: 'RL'
},
right: {
value: 'RR'
}
}
}
当前节点的值存放到value这个属性中, 左(右)子树存放到left(right)中.
这样我们很容易就能写出数组[1, null, 2, 3]的二叉树:
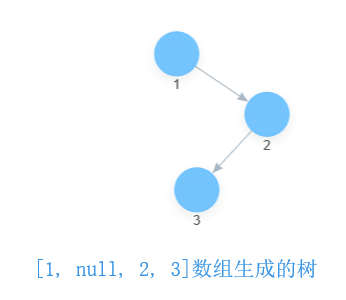
# 定义一个二叉树的节点类
通过上面的JS对象,让我们来写一个可以生成单个节点的类:
// 定义一个二叉树的节点类
class Node {
constructor(value, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
现在让我们用这个类来生成一颗简单的二叉树吧:
const tree = new Node(
'Root',
new Node(
'L',
new Node('LL'),
new Node('LR')
),
new Node(
'R',
new Node('RL'),
new Node('RR')
)
)
console.log(tree)
(这棵树在后面都会用到,大家知道后面案例的tree表示的是它就行了)
# 二叉搜索树
二叉搜索树(也叫二叉查找树)的特点:
- 左子树上所有节点的值必定全部小于根节点的值
- 右子树上所有节点的值必定全部大于根节点的值
- 左子树和右子树也分别为二叉搜索树
例如二叉搜索树:
const root = new Node(
2,
new Node(1),
new Node(
5,
new Node(4),
new Node(6)
)
);
[左子树][根][右子树]
// 对应为:
[1] [2] [4 5 6]
非二叉搜索树:
const root = new Node(
2,
new Node(3),
new Node(4)
)
[左子树][根][右子树]
// 对应为:
[3] [2] [4]
阅读全文
← 日常频繁使用的Linux命令 二叉树的镜像 →