# 二叉树
# 二叉树概述
二叉树是非常基础并且是一种非常重要的数据结构, 正和它的名字一样, 二叉树的每个节点最多有两个子树.
我们可以先来看下面的这颗二叉树, 为了方便,我这里将left用L表示, right用R表示:
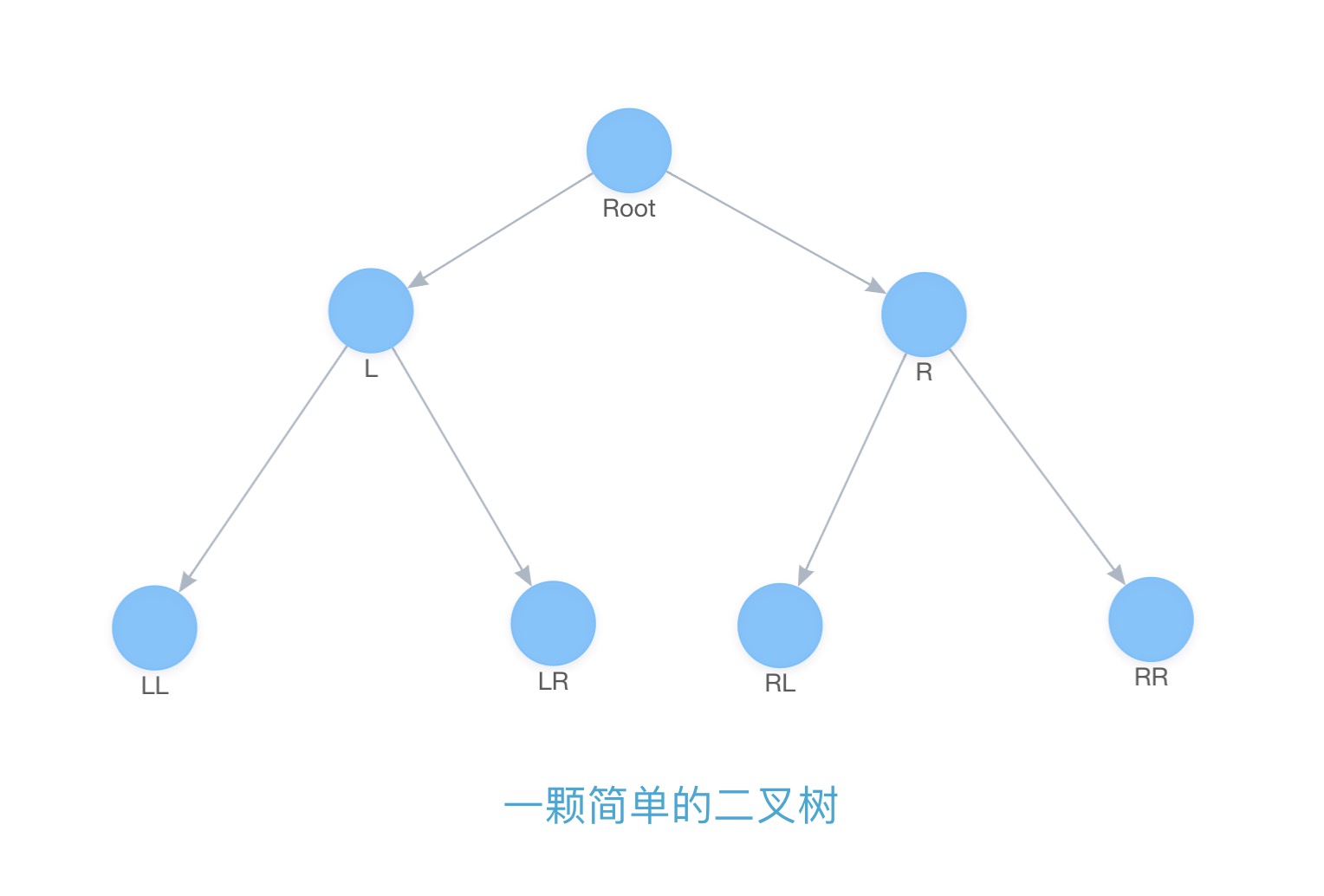
# 二叉树与JS
上面的二叉树可以用我们JavaScript的对象来进行表示, 相信大家很容易就能看懂:
var tree = {
value: "Root",
left: {
value: 'L',
left: {
value: 'LL'
},
right: {
value: 'LR'
}
},
right: {
value: 'R',
left: {
value: 'RL'
},
right: {
value: 'RR'
}
}
}
当前节点的值存放到value这个属性中, 左(右)子树存放到left(right)中.
这样我们很容易就能写出数组[1, null, 2, 3]的二叉树:
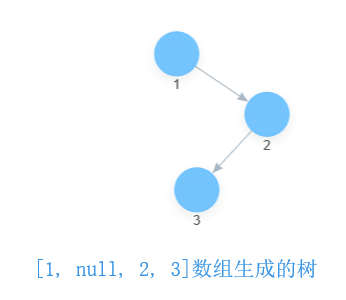
# 定义一个二叉树的节点类
通过上面的JS对象,让我们来写一个可以生成单个节点的类:
// 定义一个二叉树的节点类
class Node {
constructor(value, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
现在让我们用这个类来生成一颗简单的二叉树吧:
const tree = new Node(
'Root',
new Node(
'L',
new Node('LL'),
new Node('LR')
),
new Node(
'R',
new Node('RL'),
new Node('RR')
)
)
console.log(tree)
(这棵树在后面都会用到,大家知道后面案例的tree表示的是它就行了)
# 二叉搜索树
二叉搜索树(也叫二叉查找树)的特点:
- 左子树上所有节点的值必定全部小于根节点的值
- 右子树上所有节点的值必定全部大于根节点的值
- 左子树和右子树也分别为二叉搜索树
例如二叉搜索树:
const root = new Node(
2,
new Node(1),
new Node(
5,
new Node(4),
new Node(6)
)
);
[左子树][根][右子树]
// 对应为:
[1] [2] [4 5 6]
非二叉搜索树:
const root = new Node(
2,
new Node(3),
new Node(4)
)
[左子树][根][右子树]
// 对应为:
[3] [2] [4]
# 二叉树的遍历
# 四种遍历的概念
二叉树的遍历大范围主要分为两种:
- 深度遍历
- 广度遍历
而在深度遍历中,又分为前序、中序、后序三种遍历方法.
四种遍历的主要思想:
- 前序遍历:访问根–>遍历左子树–>遍历右子树;
- 中序遍历:遍历左子树–>访问根–>遍历右子树;
- 后序遍历:遍历左子树–>遍历右子树–>访问根;
- 广度遍历:按照层次一层层遍历;
例如一颗简单的二叉树,让我们用图形的方式来分别表示一下遍历顺序:
(数字表示的就是遍历的顺序)
| 前序 | 中序 |
|---|---|
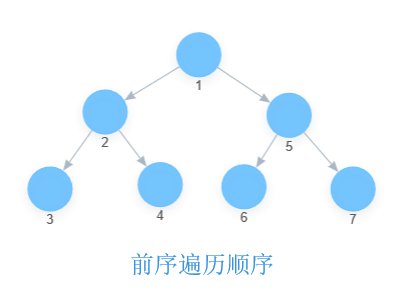 | 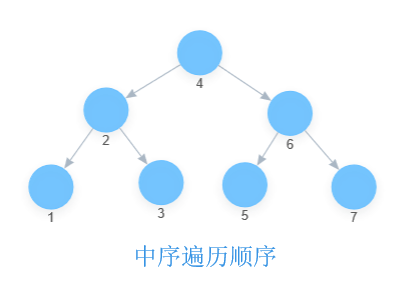 |
| 后序 | 广度 |
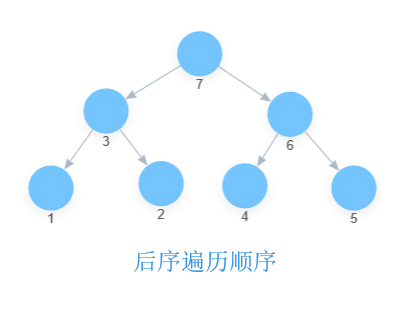 | 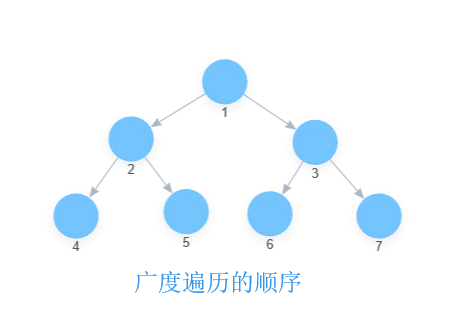 |
# 前序遍历
遍历顺序为:

首先我们来实现一下前序遍历, 你可能很容易的就想到了可以用递归的方式来实现:
递归遍历
function preOrderRec(tree) { // 前序遍历函数
let list = [] // 定义一个数组来放最终遍历结果
let preOrderRecFn = function(node) { // 定义一个函数来实现递归
if (node) { // 若是该节点存在
list.push(node.value) // 当前节点的值推进数组
preOrderRecFn(node.left) // 先遍历左子树
preOrderRecFn(node.right) // 然后遍历右子树
}
}
preOrderRecFn(tree)
return list
}
可以看到,上面preOrderRec函数接受一个tree对象, 然后判断每个节点是否存在, 若是存在则先将当前节点的值推进数组, 然后再遍历左子树, 之后再遍历右子树.
非递归遍历
function preOrderUnRec(tree) {
let list = [] // 定义一个数组来放最终遍历结果
let preOrderUnRecFn = function(node) { // 定义一个函数来遍历节点
if (node) { // 若是该节点存在
let stack = [node] // 将当前节点推入栈
while (stack.length !== 0) { // 终止条件: stack数组为空
node = stack.pop() // 取出栈中的最后一个节点
list.push(node.value) // 当前节点的值推进数组
if (node.right) stack.push(node.right) // 先将右子树节点推入栈
if (node.left) stack.push(node.left) // 再将左子树节点推入栈
}
}
}
preOrderUnRecFn(tree)
return list
}
如果你看上面的代码觉得有点生涩的话, 可以先看第一遍循环:
非递归遍历第一次循环
function preOrderUnRec(tree) {
let list = [] // 定义一个数组来放最终遍历结果
let preOrderUnRecFn = function(node) { // 定义一个函数来遍历节点
// 第一次输入的 node 为 {value: 'Root', left: {}, right: {}}
if (node) {
// 将当前节点推入栈
// 此时 stack: [ {value: 'Root', left: {}, right: {}} ]
let stack = [node]
while (stack.length !== 0) { // 终止条件: stack数组为空
// 取出栈中的最后一个节点, 此时:
// node: {value: 'Root', left: {}, right: {}}
// stack: []
node = stack.pop()
// 当前节点的值推进数组
// list: ['Root']
list.push(node.value)
// 先将右子树节点推入栈
// stack: [ {value: 'R', left: {}, right: {}} ]
if (node.right) stack.push(node.right)
// 再将左子树节点推入栈
// stack: [ {value: 'R', left: {}, right: {}}, {value: 'L', left: {}, right: {}} ]
if (node.left) stack.push(node.left)
}
}
}
preOrderUnRecFn(tree)
return list
}
经过第一次循环之后, 我们发现list中已经存放了我们想要的Root字符串.
stack数组也变成了两项:
stack: [ {value: 'R', left: {}, right: {}}, {value: 'L', left: {}, right: {}} ]
此时进入while循环的判断stack.length !== 0, 显然这个判断是为true, 所以程序又会继续往下走:
非递归遍历第二次循环
while (stack.length !== 0) { // 终止条件: stack数组为空
// 第二次循环
// 此时 stack: [ {value: 'R', left: {}, right: {}}, {value: 'L', left: {}, right: {}} ]
// node: {value: 'L', left: {}, right: {}}
// stack: [ {value: 'R', left: {}, right: {}} ]
node = stack.pop()
// 当前节点的值推进数组
// list: ['Root', 'L']
list.push(node.value)
// 先将右子树节点推入栈
// stack: [ {value: 'R', left: {}, right: {}}, {value: 'LR'} ]
if (node.right) stack.push(node.right)
// 再将左子树节点推入栈
// stack: [ {value: 'R', left: {}, right: {}}, {value: 'LR'}, {value: 'LL'} ]
if (node.left) stack.push(node.left)
}
看到这里你应该就懂了.
# 中序遍历
遍历顺序为:

遍历之后:["LL","L","LR","Root","RL","R","RR"]
递归遍历
function inOrderRec (tree) {
let list = []
let inOrderRecFn = function (node) {
if (node) {
if (node.left) inOrderRecFn(node.left)
list.push(node.value)
if (node.right) inOrderRecFn(node.right)
}
}
inOrderRecFn(tree)
return list
}
非递归遍历
非遍历我是这样考虑的:
- 会先把中间
"Root"压入栈中 - 然后开始压入
"Root"的左边节点 - 当左边节点全部都压进栈了之后,
["Root", "L", "LL"] - 要开始从栈的末位取出
value了,同时要开始把右边的也压入栈了 - 当取出
"LL"的时候,"LL"已经没有左右子节点了,所以会继续从栈的末位取出value - 也就是取出了
"L","L"还是有右节点的,所以要把"LR"压入栈 "LR"压入栈之后,"LR"也是没有左子节点的,所以会从栈的末位取出,且它又没有右子节点,就会继续取出- 继续取出
"Root",这时候再开始把node = "Root".right了,也就是要开始遍历"R"了 - 以此类推把
"R"也按上面的步骤遍历完
function inOrderUnRec (tree) {
let list = []
let inOrderUnRecFn = function (node) {
if (node) { // 当前节点存在
let stack = [] // 定义一个空的栈
while(stack.length !== 0 || node) { // 判断栈不为空或者当前节点存在
if (node) { // 若是节点存在
stack.push(node) // 将当前节点推入栈
node = node.left // 将左子树作为当前节点
} else { // 当前节点不存在(左子树为空)
node = stack.pop() // 从栈中取出节点
list.push(node.value)
node = node.right // 将右子树作为当前节点
}
}
}
}
inOrderUnRecFn(tree)
return list
}
非递归第一次遍历
let stack = [] // 定义一个空的栈
while(stack.length !== 0 || node) { // 判断栈不为空或者当前节点存在
// 此时:
// node: {value: 'Root', left: {}, right: {}}
if (node) { // 若是节点存在
// 将当前节点推入栈
// stack: [ {value: 'Root', left: {}, right: {}} ]
stack.push(node)
// 将左子树作为当前节点
// node: {value: 'L', left: {}, right: {}}
node = node.left
} else { // 当前节点不存在(左子树为空)
node = stack.pop() // 从栈中取出节点
list.push(node.value)
node = node.right // 将右子树作为当前节点
}
}
非递归第二次遍历
let stack = [] // 定义一个空的栈
while(stack.length !== 0 || node) { // 判断栈不为空或者当前节点存在
// 此时:
// node: {value: 'L', left: {}, right: {}}
if (node) { // 若是节点存在
// 将当前节点推入栈
// stack: [ {value: 'Root', left: {}, right: {}}, {value: 'L', left: {}, right: {}} ]
stack.push(node)
// 将左子树作为当前节点
// node: {value: 'LL'}
node = node.left
} else { // 当前节点不存在(左子树为空)
node = stack.pop() // 从栈中取出节点
list.push(node.value)
node = node.right // 将右子树作为当前节点
}
}
经过第二次循环之后,stack变成了[ {value: 'Root', left: {}, right: {}}, {value: 'L', left: {}, right: {}} ], 当前节点node变成了{value: 'LL'}。
这样在第四次循环的时候, node就为undefinded了,此时进入了else中,然后就达到了先遍历所有左子树,再获取根节点,最后遍历右子树的效果。
# 后序遍历
遍历顺序为:

遍历之后:["LL","LR","L","RL","RR","R","Root"]
递归遍历
function inOrderRec (tree) {
let list = []
let inOrderRecFn = function (node) {
if (node) {
if (node.left) inOrderRecFn(node.left)
if (node.right) inOrderRecFn(node.right)
list.push(node.value)
}
}
inOrderRecFn(tree)
return list
}
非递归遍历
非递归遍历的思路是:
- 通过一个对象
tmp来记录上一次入栈、出栈的节点; - 把根节点和左子树推入栈;
- 取出左子树的值;
- 推入右子树,取出右子树的值;
- 最后取出根节点的值
function postOrderUnRec (tree) {
let list = []
let postOrderUnRecFn = function (node) {
if (node) { // 当前节点存在
let stack = [node] // 将当前节点推入栈
let tmp = null // 定义一个空的对象用于盛放上一次入栈、出栈的节点
while(stack.length !== 0) { // 判断条件为 stack 不为空
tmp = stack[stack.length - 1] // 保存住栈顶的值
if (tmp.left && tmp.left !== node && tmp.right !== node) { // 若栈顶的值存在左子树且当前的节点不为左子树和右子树节点
stack.push(tmp.left) // 将左子树推入栈中
} else if (tmp.right && tmp.right !== node) {
stack.push(tmp.right)
} else { // 左子树和右子树都遍历完了之后
list.push(stack.pop().value)
node = tmp
}
}
}
}
postOrderUnRecFn(tree)
return list
}
# 广度遍历
遍历顺序:

遍历之后:["Root","L","R","LL","LR","RL","RR"]
function breadthTraversal (tree) {
let list = []
let breadthTraversalFn = function (node) {
if (node) {
var stack = [node]
while(stack.length !== 0) {
node = stack.shift() // 从栈底取出
list.push(node.value) // 添加当前节点的值至数组
if (node.left) stack.push(node.left) // 将左子树推入栈中
if (node.right) stack.push(node.right)
}
}
}
breadthTraversalFn(tree)
return list
}
广度遍历是从二叉树的根结点开始,自上而下逐层遍历;在同一层中,按照从左到右的顺序对结点逐一访问。
# 重建二叉树📕
这是《剑指offer》上一道比较经典的题, 相信你要是看懂了上面二叉树的基本用法, 那么解题就不会那么困难了. 在解每道题的时候, 你可以多想想每种遍历的特性.
# 题目描述
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。
# 解题思路
- 前序遍历的第一项一定是二叉树的根节点;
- 二叉树的根节点一定在中序遍历左子树和右子树的中间(包括没有左或右子树的情况):
[左子树][根节点][右子树]; - 用前序遍历的第一项(也就是根节点)查找到它在中序遍历的第几项,左边的就是左子树,右边为右子树;
- 根据左右子树的长度,再次划分两个序列,进一步递归.
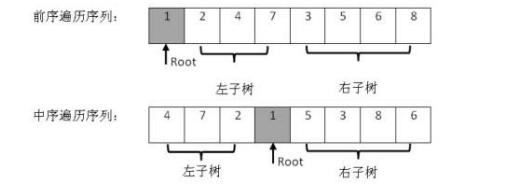
# coding
// 定义一个二叉树的节点类
class Node {
constructor(value, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
/*
* 根据前序遍历和中序遍历重构二叉树
* @param {Array} preorder
* @param {Array} inorder
* @return {Node} 重构后的树
*/
function reConstruct(preOrder, inOrder) {
if (!preOrder.length || !inOrder.length) {
return null
}
let root = preOrder[0] // 根节点的值为先序遍历的第一项
let node = new Node(root) // 新建一个节点
let i = inOrder.indexOf(root) // 查找到根节点在中序遍历中的位置
// i表示根节点在中序的位置,那么i也就表示左子树的长度了
node.left = reConstruct(preOrder.slice(1, i + 1), inOrder.slice(0, i))
node.right = reConstruct(preOrder.slice(i + 1), inOrder.slice(i + 1))
return node
}
const preArray = [1, 2, 4, 7, 3, 5, 6, 8];
const midArray = [4, 7, 2, 1, 5, 3, 8, 6];
const binTree = reConstruct(preArray, midArray);
console.log(binTree);
重构后的二叉树应该是长这样的:
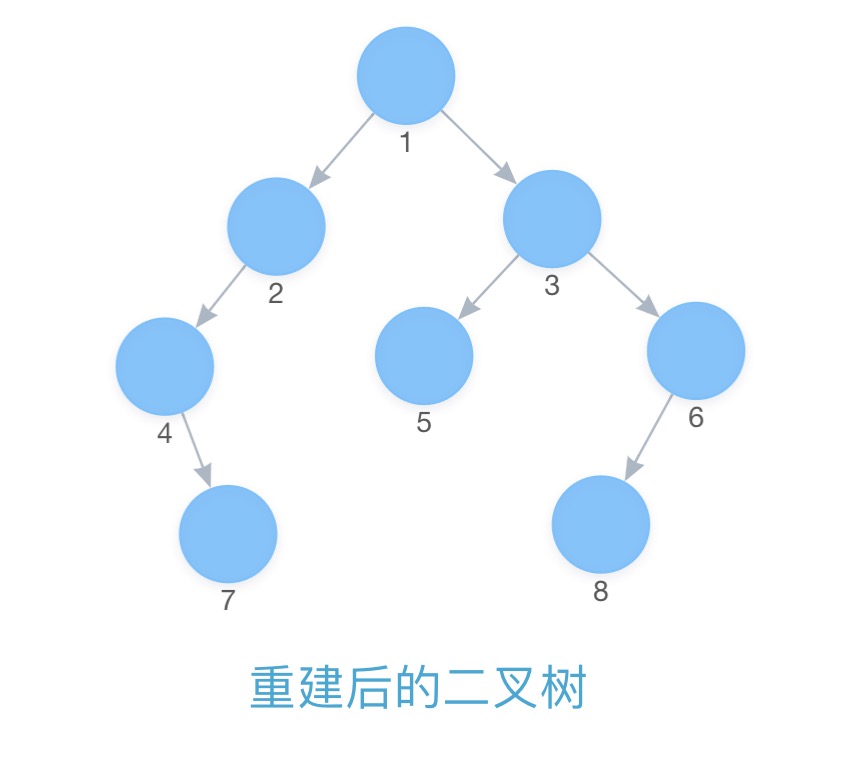
# 根据前序、中序求后序📕
# 题目描述
输入某二叉树的前序遍历和中序遍历的结果,返回后序遍历结果
# 解题思路
这道题乍一看感觉和上面的《重建二叉树》差不多,只不过多出了一步返回后序遍历。说实话,刚开始看到题目我的想法竟然是先重建出二叉树,然后再调用后序遍历的函数(┬_┬)...
但是后来想了想还是应该利用每种遍历的特性来进行解题。
前面四项还是和《重建二叉树》的思路一样:
- 前序遍历的第一项一定是二叉树的根节点;
- 二叉树的根节点一定在中序遍历左子树和右子树的中间(包括没有左或右子树的情况):
[左子树][根节点][右子树]; - 用前序遍历的第一项(也就是根节点)查找到它在中序遍历的第几项,左边的就是左子树,右边为右子树;
- 根据左右子树的长度,再次划分两个序列,进一步递归;
- 后序遍历的特性是根节点一定在最后:
[左子树][右子树][根节点]; - 创建一个数组按照
[左子树][右子树][根节点]的顺序依次推进去.
# coding
/*
* 根据前序遍历和中序遍历求后序遍历
* @param {Array} preorder
* @param {Array} inorder
* @return {Array} 后序结果
*/
function getPost (preOrder, inOrder) {
let list = [] // 定义一个栈用于存储后序结果
let getPostFn = function (preOrder, inOrder) {
if (!preOrder.length || !inOrder.length) { // 若是先序遍历或中序遍历为空则返回null
return null
}
let root = preOrder[0] // 根节点为先序遍历的第一项
let i = inOrder.indexOf(root) // 查找到根节点在中序遍历中的位置
let left = getPostFn(preOrder.slice(1, i + 1), inOrder.slice(0, i))
let right = getPostFn(preOrder.slice(i + 1), inOrder.slice(i + 1))
if (left) list.push(...left) // 先推进所有的左子树列表
if (right) list.push(...right) // 在推进所有的右子树列表
list.push(root) // 最后推入根节点
}
getPostFn(preOrder, inOrder)
return list
}
const preArray = [1, 2, 4, 7, 3, 5, 6, 8];
const midArray = [4, 7, 2, 1, 5, 3, 8, 6];
const postArray = getPost(preArray, midArray)
// [7,4,2,5,8,6,3,1]
# 判断是否子树📕
# 题目描述
输入两棵二叉树 A 和 B,判断 B 是不是 A 的子结构。
树的节点结构为:
/*
* 二叉树结点类
*/
class Node {
constructor(value, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
如下图, tree2为tree1的子结构
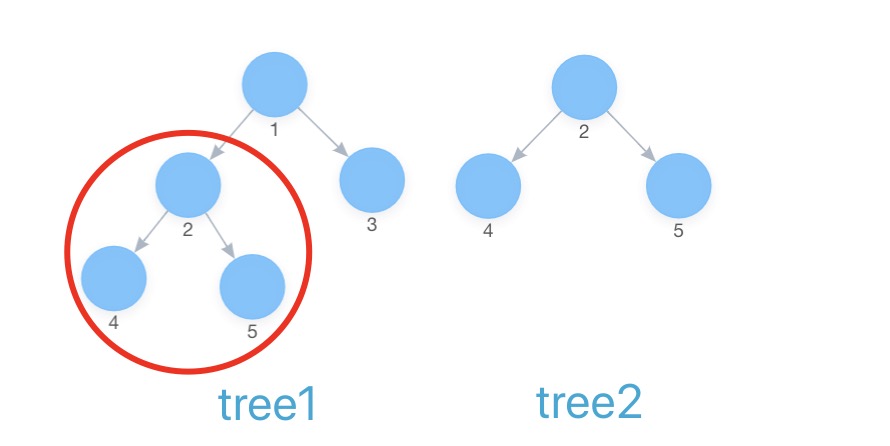
# 解题思路
假设需要判断的两颗树为tree1和tree2,需要判断tree2是否是tree1的子结构:
- 若
tree2是tree1的子结构,那么tree2的根节点必定为tree1中的某个节点, 所以要先找出这个节点; - 在
tree1中找到了这个节点后, 再判断这个节点下的所有子节点是否和tree2的子节点相同.
# coding
/*
* @param {Node} 节点1
* @param {Node} 节点2
* @return {Boolean} 树2是否是树1的子结构
*/
function isSubTree(node1, node2) {
let result = false
if (node1 && node2) {
if (node1.value === node2.value) { // 若是节点的值相同
result = doesNode1HasNode2(node1, node2) // 判断后面的子节点结构是否相同
}
if (!result) { // 若是根节点的值不同, 则用树1的左子树遍历
result = isSubTree(node1.left, node2)
}
if (!result) { // 用树1的右子树遍历
result = isSubTree(node1.right, node2)
}
}
return result
}
/*
* node2是否是node1的子树: node1和node2的根节点的值是否相同
* @param {Node} 节点1
* @param {Node} 节点2
* @return {Boolean} 树2是否是树1的子结构
*/
function doesNode1HasNode2(node1, node2) {
if (!node2) { // 若是node2全遍历完了则说明node1包含node2
return true
}
// 若是node1遍历完了 或者 两个节点的值不相同
if (!node1 || node1.value !== node2.value) {
return false
}
// 节点的左子树和右子树都得相同
return (
doesNode1HasNode2(node1.left, node2.left) &&
doesNode1HasNode2(node1.right, node2.right)
)
}
const tree1 = new Node(0, new Node(1, new Node(3)), new Node(2));
const tree2 = new Node(1, new Node(3));
console.log(isSubTree(tree1, tree2));
# 二叉树的镜像📕
# 题目描述
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如🌰:
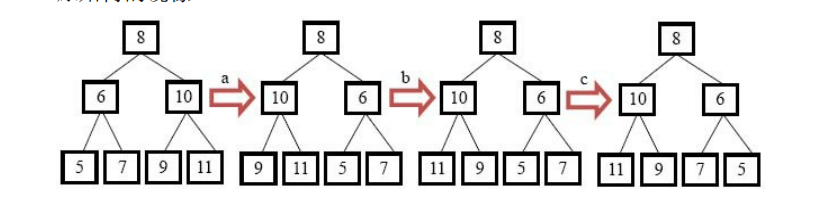
# 解题思路
- 根节点不需要变;
- 二叉树的左子树的节点与右子树的节点进行交换;
- 遍历交换子节点.
# coding
解法一
我开始的想法是, 每次都重新生成一个新的节点然后赋值.但实际上这样解法不是最优的, 每次都产生多余的对象.
/*
* 二叉树结点类
*/
class Node {
constructor(value, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
/*
* 传入一个二叉树, 返回二叉树的镜像
* param {Node} 二叉树
* return {NOde} 二叉树镜像
*/
function mirrorBinaryTree(node) {
if (!node) return null
let tree = new Node(node.value) // 生成一个新的节点
tree.left = mirrorBinaryTree(node.right) // 新节点的左子树为原节点的右子树
tree.right = mirrorBinaryTree(node.left)
return tree
}
const tree3 = new Node(8, new Node(6, new Node(5), new Node(7)), new Node(10, new Node(9), new Node(11)))
console.log(tree3)
console.log(mirrorBinaryTree(tree3))
解法二
可以直接找进行左右节点的交换:
/*
* 传入一个二叉树, 返回二叉树的镜像
* param {Node} 二叉树
* return {NOde} 二叉树镜像
*/
function mirrorBinaryTree(node) {
if (!node) return null
let left = node.left
node.left = node.right
node.right = left
if (node.left) mirrorBinaryTree(node.left)
if (node.right) mirrorBinaryTree(node.right)
}
const tree3 = new Node(8, new Node(6, new Node(5), new Node(7)), new Node(10, new Node(9), new Node(11)))
mirrorBinaryTree(tree3)
console.log(tree3)
# 二叉搜索树的后序遍历序列📕
# 题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
# 解题思路
- 搜索二叉树的特点:左子树的值一定小于根节点的值,右子树的值一定大于根节点的值,左右子树也为搜索二叉树
- 后序遍历的特点:最后一个元素一定是根元素,排列的顺序是
[左子树][右子树][根节点]。
例如🌰:
[1, 5, 4, 3, 2]; // true 左子树: [1],右子树: [5,4,3], 根节点: 2
[1, 5, 2, 4, 3]; // false
# coding
解法一
- 传递进来数组的最后一项是根节点,把它从数组中
pop()出来 - 然后可以用
findIndex()查找出数组中大于根节点的那个下标rightIdx,这个下标就是左子树和右子树的分割下标 - 在下标左边为左子树,下标及下标右边为右子树
- 利用数组的
every()判断左子树的每一项是不是都小于根节点且左子树是不是也是二叉搜索树,同理判断右子树的每一项是不是都大于根节点且右子树是不是也是二叉搜索树
/*
* 判断某个数组是不是某搜索二叉树的后序遍历结果
* param {Array}
* return {Boolean}
*/
function isBST (postOrder) {
let isBSTFn = function (postOrder) {
// 若长度为0 则也判断为true
if (postOrder.length === 0) {
return true;
}
let res = true;
if (postOrder) {
let root = postOrder.pop(); // 根节点
let rightIdx = postOrder.findIndex(item => item > root);
let left = postOrder.splice(0, rightIdx);
let right = postOrder;
if (left) {
res = left.every(item => item < root) && isBSTFn(left);
}
if (right) {
res = right.every(item => item > root) && isBSTFn(right);
}
}
return res;
}
return isBSTFn(postOrder)
}
console.log(isBST([5, 4, 3, 2, 1])); // true 左子树: [], 右子树: [5,4,3,2], 根节点: 1
console.log(isBST([1, 5, 4, 3, 2])); // true 左子树: [1],右子树: [5,4,3], 根节点: 2
console.log(isBST([1, 5, 2, 4, 3])); // false
解法二
/*
* 判断某个数组是不是某搜索二叉树的后序遍历结果
* param {Array}
* return {Boolean}
*/
function isBST (postOrder) {
// 若长度为0 则也判断为true
if (postOrder.length === 0) {
return true;
}
const len = postOrder.length
let root = postOrder[len - 1], // 最后一位为根节点的值
i, // 左子树的最后一位的下标
j; // 右子树的第一位的下标
for (i = 0; i < len - 1 && postOrder[i] < root; ++i);
for (j = i; j <len - 1 && postOrder[j] > root; ++j);
if (j !== len - 1) { // 若还未遍历完,则说明不是左边部分小,右边部分大,不符合后序遍历
return false;
}
let left = isBST(postOrder.slice(0, i)); // 继续遍历左子树
let right = isBST(postOrder.slice(i, len - 1));
return left && right;
}
console.log(isBST([5, 4, 3, 2, 1])); // true 左子树: [], 右子树: [5,4,3,2], 根节点: 1
console.log(isBST([1, 5, 4, 3, 2])); // true 左子树: [1],右子树: [5,4,3], 根节点: 2
console.log(isBST([1, 5, 2, 4, 3])); // false
# 二叉搜索树的第k个节点📕
# 题目描述
给定一棵二叉搜索树,请找出其中的第k小的节点。 例如, (5,3,7,2,4,6,8) 中,按结点数值大小顺序第三小结点的值为4。
# 解题思路
- 利用二叉搜索树中序遍历就是按从小到大的特性;
- 中序遍历排好序后返回对应
k-1下标的那一项节点。
# coding
/*
* 二叉树结点类
*/
class Node {
constructor(value = 0, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
/**
* 二叉搜索树的第k个节点
* @param {Node} root
* @param {Number} target
*/
function KthNode(root, target) {
const arr = []
inOrderRec(root, arr)
if (target > 0 && target <= arr.length) {
return arr[target - 1]
}
return null;
}
/*
* 二叉树中序递归遍历
*/
function inOrderRec (node, arr) {
if (node) {
inOrderRec(node.left, arr)
arr.push(node)
inOrderRec(node.right, arr)
}
}
/*
* 二叉树中序非递归遍历
*/
// function inOrderUnRec (node) {
// let list = [];
// let stack = [];
// while (stack.length !== 0 || node) {
// if (node) {
// stack.push(node);
// node = node.left;
// } else {
// node = stack.pop();
// list.push(node);
// node = node.right;
// }
// }
// return list;
// }
const root = new Node(
2,
new Node(1),
new Node(
5,
new Node(4),
new Node(6)
)
);
console.log(KthNode(root, 3))
// { value: 4, left: null, right: null }
# 二叉树的最大深度📕
# 题目描述
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
# 解题思路
- 深度遍历二叉树,比较出左子树的最大深度和右子树的最大深度
- 二叉树的最大深度为上面比较的结果 + 1.
# coding
解法一: 较为复杂
实现上和 二叉搜索树的第k个节点有点类似:
class Tree {
constructor(value = 0, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
function getMaxDeep(tree) {
if (!tree) return 0;
let deep = 0, // 定义一个路径的深度
maxDeep = 0; // 定义最大的深度
function _getMaxDeep(node) {
if (!node) return; // 若是没有节点则直接返回
deep++;
let isLeaf = !node.left && !node.right; // 判断是否是叶子节点
if (isLeaf && deep > maxDeep) { // 若是叶子节点且当前路径的深度大于最大的深度
maxDeep = deep;
}
if (node.left) { // 若是有左子树节点则遍历
_getMaxDeep(node.left)
}
if (node.right) {
_getMaxDeep(node.right)
}
deep--; // 遍历完之后将deep重置
}
_getMaxDeep(tree);
return maxDeep;
}
const tree = new Tree(1, new Tree(2, new Tree(4), new Tree(6, new Tree(7))), new Tree(3, null, new Tree(5)));
console.log(getMaxDeep(tree))
// 4
解法二:简单明了
function treeDepth (node) {
return !node ? 0 : Math.max(treeDepth(node.left), treeDepth(node.right)) + 1;
}
const tree = new Tree(1, new Tree(2, new Tree(4), new Tree(6, new Tree(7))), new Tree(3, null, new Tree(5)));
console.log(treeDepth(tree))
// 4
# 二叉树的最小深度📕
# 题目描述
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
# 解题思路
解题思路与二叉树的最大深度差不多 ,但是有一点需要注意,那就是如下这种情况:
1
/
2
这种情况的最小深度应该是2。
所以如果还是和求「最大深度」一样的话,就不满足了。
因此需要多加一层判断:判断若是一方子树有,另一方子树没有的时候,应该返回有的那方子树的深度再加1。
# coding
class Tree {
constructor(value = 0, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
function getMinDeep(tree) {
if (!node) return 0;
let left = getMinDeep(node.left);
let right = getMinDeep(node.right);
if ((left && !right) || (!left && right)) return (left || right) + 1;
return Math.min(left, right) + 1;
}
const tree = new Tree(1, new Tree(2, new Tree(4), new Tree(6, new Tree(7, new Tree(9)))), new Tree(3, new Tree(8), new Tree(5)));
const tree2 = new Tree(1, new Tree(2), new Tree(3, new Tree(4), new Tree(5)))
const tree3 = new Tree(1, new Tree(2));
console.log(getMinDeep(tree)) // 3
console.log(getMinDeep(tree2)) // 2
console.log(getMinDeep(tree3)) // 2
# 二叉树的序列化与反序列化📕
# 题目描述
请实现两个函数,分别用来序列化和反序列化二叉树
例如给定的一棵树的结构为:
要求返回序列化为1,2,#,#,3,4,#,#,5,#,#
# 解题思路
序列化思路
- 判断节点的值是否存在,若是不存在则需要用一个特殊符号来代替,如
#符号; - 序列化实际就是将二叉树进行前序遍历
反序列化思路
- 判断值为
#的项,将其转换为null; - 输入的数组为二叉树的前序遍历,利用这一特性进行左右子树的赋值
# coding
class Node {
constructor(value = 0, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
/*
* 序列化二叉树
* param {Tree} tree 二叉树
* param {Array} arr 序列化之后的数组
* return {String} 返回序列化之后字符串
*/
function serialize(node, arr = []) {
if (!node) { // 判断该节点有没有,没有则用特殊符号 # 代替
arr.push('#');
} else {
arr.push(node.value); // 当前节点的值
serialize(node.left, arr) // 分别遍历左右子树
serialize(node.right, arr)
}
return arr.join(','); // 将返回的数组进行逗号连接(若想返回数组则不用.join(','))
}
/*
* 反序列化二叉树,通过字符串
* param {String} str 序列化之后的字符串
*/
function DeSerializeByStr (str) {
if (!str) return null;
return DeserializeByArr(str.split(','))
}
/*
* 反序列化二叉树,通过数组
* param {Array} arr 序列化之后的数组
*/
function deSerializeByStr (str) {
if (!str) return null;
let arr = str.split(',');
let deSerializeByArr = function (arr) {
let currentNode = arr.shift(); // 第一项为根
if (currentNode === '#') {
return null;
} else {
let node = new Node(currentNode);
node.left = deSerializeByArr(arr);
node.right = deSerializeByArr(arr);
return node;
}
}
return deSerializeByArr(arr);
}
const tree = new Node(1, new Node(2), new Node(3, new Node(4), new Node(5)))
console.log(serialize(tree))
console.log(deSerializeByStr('1,2,#,#,3,4,#,#,5,#,#'))
# 二叉树中和为某一值的路径📕
# 题目描述
输入一棵二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
# 解题思路
- 每次到新的节点上,都记录新的节点的值;
- 判断新的节点是否是叶子节点,若是叶子节点则判断路径上节点值的总和是否符合条件;若不是,则继续递归处理左右子树;
- 最后需要将新节点的信息清除。
# coding
class Node {
constructor (value, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
/*
* 根据 target 返回某一路径
* param {Tree} tree
* param {Number} target
*/
function searchPath (tree, target) {
let sum = 0, // 路径上的节点的值的总和
paths = []; // 存放所有满足条件的路径
function _searchPath (node, path) {
if (node === null) {
return
}
sum = sum + node.value; // 计算总和
path.push(node); // 将当前节点推入路径中
// 判断是否是叶子节点
const isLeaf = node.left === null && node.right === null;
if (isLeaf && sum === target) { // 若是叶子节点且路径上的节点满足条件则记录这条路径
paths.push([...path])
}
if (node.left !== null) { // 向左子树递归
_searchPath(node.left, path)
}
if (node.right !== null) {
_searchPath(node.right, path)
}
sum = sum - node.value; // 把当前节点从路径中移除, 达到重置的效果
path.pop();
}
_searchPath(tree, []);
return paths;
}
const tree = new Node(1, new Node(2, new Node(4), new Node(6)), new Node(3, null, new Node(5)));
console.log(searchPath(tree, 9))
# 从上到下打印二叉树📕
例如有棵树是这样的:
1
/ \
2 3
/ \ / \
4 6 7 5
该课树转换为JS代码:
class Node {
constructor (value, left = null, right = null) {
this.value = value;
this.left = left;
this.right = right;
}
}
const tree = new Node(1, new Node(2, new Node(4), new Node(6)), new Node(3, new Node(7), new Node(5)));
(为后面三题的前置条件)
# 题目1-不分行从上到下打印
# 题目描述
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
需要输出:
[1, 2, 3, 4, 6, 7, 5]
# 解题思路
这道题其实很简单啦,看这输出结果,不就是求二叉树的广度遍历吗?
# coding
OK👌,直接开搞:
function print(node) {
let list = [];
let stack = [node];
while (stack.length !== 0) {
node = stack.shift();
list.push(node.value);
if (node.left) stack.push(node.left);
if (node.right) stack.push(node.right);
}
return list;
}
console.log(print(tree));
# 题目2-把二叉树打印成多行
# 题目描述
从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
需要输出:
[
[1],
[2, 3],
[4, 6, 7, 5]
]
# 解题思路
- 总体来说还是需要使用广度遍历
- 需要定义一个二维数组
result来盛放每一层的结果,也就是最后的输出结果 - 需要一个数组
tempArr来盛放当前这层所有节点的值 - 需要一个变量来记录当前这层的节点数量
currentNums - 需要一个变量来记录当前这层的孩子节点的数量
childNums - 当前层遍历完成后开始遍历孩子节点,
currentNums赋值为childNums,childNums赋值为0
# coding
function print (node) {
let result = [];
let tempArr = [];
let currentNums = 1;
let childNums = 0;
let stack = [node];
while (stack.length !== 0) {
node = stack.shift();
tempArr.push(node.value);
if (node.left) {
stack.push(node.left);
childNums++;
}
if (node.right) {
stack.push(node.right);
childNums++;
}
currentNums--;
if (currentNums === 0) {
currentNums = childNums;
childNums = 0;
result.push(tempArr);
tempArr = [];
}
}
return result;
}
# 题目3-按之字形顺序打印二叉树
# 题目描述
请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。
需要输出:
[
[1],
[3, 2],
[4, 6, 7, 5]
]
# 解题思路
解法一
可以将题目2中得到的二维数组处理一下:把偶数层的数组使用reserve逆序排一下就行了。
解法二
每一层是从左到右打印还是从右到左打印是由谁决定的呢?
例如我们定义了一个数组stack用来放某个节点下的子节点。
这里有一颗超级简单的树:
1
/ \
2 3
stack是长[2, 3]或是长[3, 2],其实只是由push的顺序决定的而已。
- 若当前层为奇数层,从左到右打印,同时填充下一层,从右到左打印(先填充左孩子节点再填充右孩子节点)。
- 若当前层为偶数层,从右到左打印,同时填充下一层,从左到右打印(先填充右孩子节点再填充左孩子节点)。
# coding
解法一
function print (node) {
let result = [];
let tempArr = [];
let currentNums = 1;
let childNums = 0;
let stack = [node];
while (stack.length !== 0) {
node = stack.shift();
tempArr.push(node.value);
if (node.left) {
stack.push(node.left);
childNums++;
}
if (node.right) {
stack.push(node.right);
childNums++;
}
currentNums--;
if (currentNums === 0) {
currentNums = childNums;
childNums = 0;
result.push(tempArr);
tempArr = [];
}
}
result = result.map((arr, idx) => {
return (idx + 1) % 2 === 0 ? arr.reverse() : arr;
})
return result;
}
解法二
function print(node) {
const result = [];
const oddStack = [];
const evenStack = [];
let temp = [];
if (node) {
oddStack.push(node)
while (oddStack.length !== 0 || evenStack.length !== 0) {
while (oddStack.length !== 0) {
const current = oddStack.shift();
temp.push(current.value);
if (current.right) {
evenStack.push(current.right);
}
if (current.left) {
evenStack.push(current.left);
}
}
if (temp.length > 0) {
result.push(temp);
temp = [];
}
while (evenStack.length !== 0) {
const current = evenStack.shift();
temp.push(current.value);
if (current.left) {
oddStack.push(current.left)
}
if (current.right) {
oddStack.push(current.right)
}
}
if (temp.length > 0) {
result.push(temp);
temp = [];
}
}
}
return result;
}